이쁜왕자 만쉐~~

'역수'에 대한 내용의 중학교 수학 문제이다.바로 풀어 보면 아래와 같다. 세개의 식에 대해서 역수를 취해서 정리하면 이렇게 되고, 이를 다 더한 뒤 2로 나누면, 간단히 답이 나온다. 그런데, 이거 '문제 자체가 틀렸다'.두번째 식을 정리하면 이렇게 되고, 이를 최종식에 대입하면, 즉, a 가 무한대 여야 성립하는 식이다. 그리고, 무한대는 수가 아니다. 이 연립방정식을 만족하는 a,b,c 를 실수 범위에서는 구할 수 없고, 그러므로 1/a + 1/b + 1/c 도 계산할 수 없다.무한대도 수로 취급하는 Surreal number 나 Hyperreal number 를 동원하면 어찌 되기야 하겠지만, 중학교 수학 수준은 한참 넘어간다.

인터넷을 돌아 다녀 보면 1^x = 2 라는 문제가 있고, 이것의 해를 어떻게 구하는지에 대한 설명이 나온다. 사실 고등학교 수학 수준에서는 어떤 x 에 대해서도 1^x = 1 이어야 하므로, 이 문제의 해는 존재하지 않는다. 문제는, 이 것이 대학교 수준으로 가서 '복소해석학'과 결합되면 신기하게도 해가 존재한다. 이는 log (-1) 이 고등학교 수준에서는 정의되지 않지만, 대학교에서는 정의할 수 있는 것과 비슷하다. https://www.valken.net/573 참고 여튼 이 식의 답을 얻기 위해서는 '오일러의 공식'에서 유래되는 e^(2n pi i) = 1 이 필요하다. 그냥 냅다 이 식을 집어 넣고 양변에 log 를 취해서 답을 구하면, 아래와 같은 해를 구할 수 있다. 사실 중간에 2n pi..

제한 조건 1. 오직 사칙연산(+-*/) 와 괄호만 허용함. 2. 지수 사용 불가능 (예: 10^10 ) 3. 붙여 쓰기 불가능 (예: 1010 ) 그냥 끄적끄적 거리며 만들어 보니 11개 짜리는 비교적 쉽게 나왔다. (10+10)*(10*10) + 10 + 10 + (10+10+10+10)/10 = 2024 사실 지수가 허용되면, 10*10*10 = 1000, 2^10 = 1024 라는 점을 이용해서 10*10*10 + ((10+10)/10) ^ 10 = 2024 라는 7개짜리 답이 만들어 졌다. 하지만, 지수를 불허해서 탈락. 이리 저리 시도해본 결과, (10+10)*(10*10) = 2000 에서 시작해서, 6개 이하로 24를 어떻게 만드는 지를 고민하는 방향으로 가게 되었다. 20 + 4 = 24..

직소 퍼즐의 난이도는 조각의 수가 늘어 날수록 기하급수적으로 난이도가 폭발한다. 예를 들어 1000피스 퍼즐에 비해서 2000 피스 퍼즐은 2배 어려운 것이 아니라, 그 몇배로 난이도가 급 상승한다. 그러면 동일하게 1000피스 퍼즐이라고 할때, 어떤 퍼즐이 더 어려울까? 개인적으로 완성해본 퍼즐 중에서는 위 사진의 러브레터 퍼즐이 정말 힘들었는데, 글자와 사람, 나무를 맞추고 난 다음에는 거진 500개 넘는 조각이 흰색부터 옅은 하늘색까지 정말 구분도 쉽지 않은 비슷비슷한 수준이어서 정말 힘들었었다. 이처럼 색의 구분이 되지 않으면, 정말 모양만으로 맞추어야 하기 때문에 난이도가 급격하게 상승한다. 개인적으로 아예 시도조차 안했던 퍼즐이 하나 있다면, 뤽베송 감독의 그랑블루(LE GRAND BLEU) ..

직소 퍼즐(Jigsaw puzzle) 또는 조각 퍼즐이란 굴곡이 있는 조각을 맞추어 전체 그림을 완성하는 퍼즐을 뜻한다. 직소 퍼즐의 경우 조각의 수가 다양해서, 유아부터 시작해서 성인까지 스펙트럼이 아주 넓다. 100피스 이하의 퍼즐은 어린이들도 비교적 쉽게 도전해 볼 수 있다. 반면, 성인을 대상으로 하는 것은 보통 1000피스 정도 된다. 물론 1000피스 퍼즐만 되더라도 상당히 난이도가 있기 때문에, 300피스, 500피스 같은 중간단계의 퍼즐도 다수 존재한다. 참고로 현재 확인된 가장 큰 크기의 퍼즐은 무려 51300피스 짜리 이다. 보통 32000 피스 퍼즐이 최대 크기라고 알려져 있지만, 검색해 보니 5만 피스가 넘어가는 저 제품이 검색되었다. 다만, 현재 시점에서 구할 수 있는지는 미지수이..

오랫만에 심신의 안정을 되찾자는 마음에 사놓고 방치했던 1000 피스 직소 퍼즐을 꺼내 들었다. 직소 퍼즐을 여러개 완성해 보았는데, 예전에 워낙 어려운 걸 맞추다가 고생한 덕분에, 그래도 쉬운걸 고른다고 골랐던 것이었다. 하지만, 실제로 열어서 조각들의 모습을 본 결과 결코 쉽지 않은 난이도였고, 테두리만 만든 채 그대로 다시 봉인했었다. 그리고, 이번에 다시 꺼내 들어 맞추기로 했다. 역시 정석대로 색상 분류 작업부터 시작했다. 벚꽃색, 연두색, 검정색, 파랑색 등등.. 사람의 형태와 큰 벚꽃까지는 비교적 쉬웠지만, 그 다음부터는 역시 난이도가 급상승 하였다. 무엇보다 더 힘들게 한것은 허리통증. 바닥에 펼쳐 놓은채 허리를 숙이고 눈이 빠져라 보고 있으려니 허리가 장난이 아니게 아팠다. 그래도, 완성..

여기 9개의 자연수가 있습니다. 이 9개의 자연수는 모두 9보다 작거나 같습니다. 이 9개의 자연수를 모두 더하면 45입니다. 이 9개의 자연수를 모두 곱하면 9! (=362880) 입니다. 그런데, 이 9개의 자연수는 1,2,3,4,5,6,7,8,9 는 아닙니다. 이 9개의 자연수는 무엇일까요? 더보기 정답 : 1 2 4 4 4 5 7 9 9

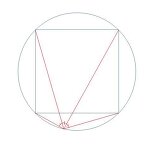
먼저 임의의 정사각형을 그립니다. 그리고, 이 정사각형에 외접하는 외접원을 그립니다. 그리고, 그 원에서 임의의 한 점을 잡습니다. 그 다음 그 점으로 부터 정사각형의 각 꼭지점으로 선분을 긋습니다. 1. 가장 큰 각을 제외한 3개의 각은 왜 같은지를 설명하시오. 2. 그래서 그 각은 몇도일까요?

마치 혜성처럼 보이는 이 그림은 '골드바흐의 추측'이라는 수학 난제와 관련이 있는 그래프이다. 수학 문제를 풀었을 뿐인데, 이런 멋진 그림이 나오는 거 보면 수학은 정말 신기한 분야이다. '골드바흐의 추측'은 아래와 같다. 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다. 4부터 하나씩 조사해 보면 이 추측이 성립함을 알 수 있다. 어느 수학자가 10^20 까지 컴퓨터로 확인했는데, 모두 성립함을 확인 하였다. 하지만, 모든 수에 대해서 증명된 것은 아니다. 4 = 2 + 2 6 = 3 + 3 8 = 3 + 5 10 = 5 + 5 12 = 5 + 7 14 = 7 + 7 16 = 5 + 11 18 = 7 + 11 20 = 7 + 13 문제 자체는 정말 이해하기 쉽지만, 증명되지 않은 수학 난제이다..

철수는 수직선의 0 의 위치에 있다. 그리고, 6면체 주사위를 굴린 뒤 그 수만큼 이동하는 것을 반복한다. 철수가 1에서 멈출 확률을 첫번째 주사위가 1이 나오는 경우 밖에 없으므로 1/6 이다. 철수가 2에서 멈출 확률은 0 에서 1,1 이 나오거나, 0 에서 2가 나오는 경우가 있으므로 7/36 이다. 충분히 큰 양의 정수 N 에 대해서 철수가 N 에서 멈출 확률을 구하라. ------------------------------ 정답을 먼저 말하면 1/3.5 = 약 0.2587 이다. 주사위를 한번 굴릴때마다 1~6 의 평균값인 3.5 만큼 이동하게 되는데, 반대로 한곳에서 멈출 확률은 이 수의 역수인 1/3.5 이 된다.